2. Poisson 方程 II#
2.1. 构造等参元#
Firedrake 中坐标是通过函数 Function 给出的, 可以通过更改该函数的值来移动网格或者构造等参元对应的映射.
2.1.1. 修改网格坐标 (移动网格)#
坐标的存储 (numpy 数组)
mesh = RectangleMesh(10, 10, 1, 1)
mesh.coordinates.dat.data
mesh.coordinates.dat.data_ro
mesh.coordinates.dat.data_with_halos
mesh.coordinates.dat.data_ro_with_halos
单进程运行时 data 和 data_with_halos 相同. 关于 halos 请参考 https://op2.github.io/PyOP2/mpi.html.
from firedrake import RectangleMesh, triplot
import numpy as np
import matplotlib.pyplot as plt
# test_mesh = UnitDiskMesh(refinement_level=3)
test_mesh = RectangleMesh(10, 10, 1, 1)
fig, ax = plt.subplots(1, 2, figsize=[8, 4])
handle = triplot(test_mesh, axes=ax[0])
theta = np.pi/6
R = np.array([[np.cos(theta), - np.sin(theta)],
[np.sin(theta), np.cos(theta)]])
# test_mesh.coordinates.dat.datas[:] = test_mesh.coordinates.dat.data_ro[:]@R
test_mesh.coordinates.dat.data_with_halos[:] = test_mesh.coordinates.dat.data_ro_with_halos[:]@R
handle = triplot(test_mesh, axes=ax[1])
fig.tight_layout()
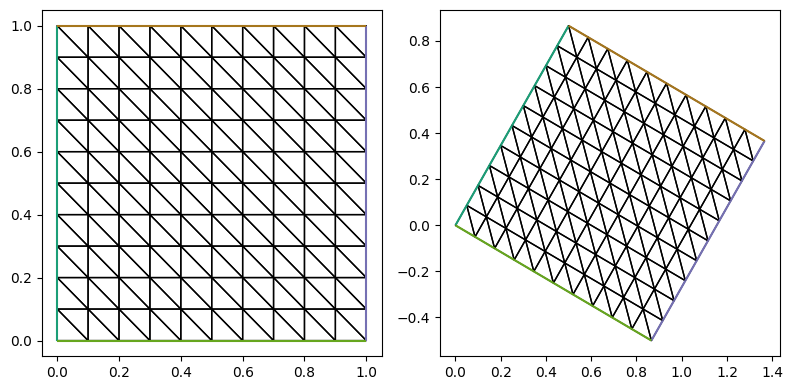
2.1.2. 简单映射边界点#
等参元映射通过更改坐标向量场实现: 从线性网格开始构造, 把边界上的自由度移动到边界上. 以单位圆为例:
def points2bdy(points):
r = np.linalg.norm(points, axis=1).reshape([-1, 1])
return points/r
def make_high_order_mesh_map_bdy(m, p):
coords = m.coordinates
V_p = VectorFunctionSpace(m, 'CG', p)
coords_p = Function(V_p, name=f'coords_p{i}').interpolate(coords)
bc = DirichletBC(V_p, 0, 'on_boundary')
points = coords_p.dat.data_ro_with_halos[bc.nodes]
coords_p.dat.data_with_halos[bc.nodes] = points2bdy(points)
return Mesh(coords_p)
2.1.3. 同时移动边界单元的内点#
等参元映射通过更改坐标向量场实现: 从线性网格开始构造, 把边界上的自由度移动到边界上, 同时移动边界单元的内部自由度.
def make_high_order_mesh_simple(m, p):
if p == 1:
return m
coords_1 = m.coordinates
coords_i = coords_1
for i in range(2, p+1):
coords_im1 = coords_i
V_i = VectorFunctionSpace(m, 'CG', i)
bc = DirichletBC(V_i, 0, 'on_boundary')
coords_i = Function(V_i, name=f'coords_p{i}').interpolate(coords_im1)
coords_i.dat.data_with_halos[bc.nodes] = \
points2bdy(coords_i.dat.data_ro_with_halos[bc.nodes])
return Mesh(coords_i)
这是一个简单的实现, 并不完全符合文献 [Len86] 中等参元映射构造方式, 一个完整的实现方式见文件 py/make_mesh_circle_in_rect.py 中的函数 make_high_order_coords_for_circle_in_rect: 该函数实现了内部具有一个圆形界面的矩形区域上的等参映射.
2.1.4. 数值实验#
假设精确解为 \(u = 1 - (x^2 + y^2)^{3.5}\).
在 jupyter-lab 执行运行文件 possion_convergence_circle.py
%run py/possion_convergence_circle.py -max_degree 3 -exact "1 - (x[0]**2 + x[1]**2)**3.5"
或在命令行运行
python py/possion_convergence_circle.py -max_degree 3 -exact "1 - (x[0]**2 + x[1]**2)**3.5"
有输出如下:
$ python py/possion_convergence_circle.py -max_degree 3 -exact "1 - (x[0]**2 + x[1]**2)**3.5"
Exact solution: 1 - (x[0]**2 + x[1]**2)**3.5
p = 1; Use iso: False; Only move bdy: False.
Rel. H1 errors: [0.21472147 0.10953982 0.05505367]
orders: [0.99748178 1.00490702]
Rel. L2 errors: [0.02973733 0.00764636 0.00192565]
orders: [2.01284532 2.01420929]
p = 2; Use iso: False; Only move bdy: False.
Rel. H1 errors: [0.02567607 0.00823192 0.00274559]
orders: [1.68586184 1.60384374]
Rel. L2 errors: [0.00804638 0.00197793 0.00048968]
orders: [2.07953304 2.0391775 ]
p = 2; Use iso: True; Only move bdy: False.
Rel. H1 errors: [0.02049517 0.00516031 0.0012846 ]
orders: [2.04399704 2.03112667]
Rel. L2 errors: [1.32436157e-03 1.65779996e-04 2.05806815e-05]
orders: [3.07968268 3.04739627]
p = 3; Use iso: False; Only move bdy: False.
Rel. H1 errors: [0.01465085 0.00517696 0.00182789]
orders: [1.54172011 1.52063516]
Rel. L2 errors: [0.00786267 0.00195543 0.00048687]
orders: [2.06225863 2.03084755]
p = 3; Use iso: True; Only move bdy: True.
Rel. H1 errors: [2.88080070e-03 5.12223863e-04 9.06665015e-05]
orders: [2.5595478 2.52924769]
Rel. L2 errors: [1.06566715e-04 9.18124027e-06 7.97431433e-07]
orders: [3.63334435 3.56916446]
p = 3; Use iso: True; Only move bdy: False.
Rel. H1 errors: [1.02564343e-03 1.25126956e-04 1.52758197e-05]
orders: [3.11780384 3.07186088]
Rel. L2 errors: [4.46595130e-05 2.69981492e-06 1.63948920e-07]
orders: [4.15838886 4.09188043]
2.2. 间断有限元方法#
2.2.1. UFL 符号#
+:u('-')-:u('+')avg:
(u('+') + u('-'))/2jump:
jump(u, n) = u('+')*n('+') + u('-')*n('-')jump(u) = u('+') - u('-')FacetNormal:
边界法向
CellDiameter:
网格尺寸
2.2.2. UFL 测度#
ds外部边dS内部边
2.2.3. 变分形式#
其中 \([vn] = v^+n^+ + v^-n^-, \{u\} = (u^+ + u^-)/2\)
from firedrake import *
import matplotlib.pyplot as plt
mesh = RectangleMesh(8, 8, 1, 1)
DG1 = FunctionSpace(mesh, 'DG', 1)
u, v = TrialFunction(DG1), TestFunction(DG1)
x, y = SpatialCoordinate(mesh)
f = sin(pi*x)*sin(pi*y)
h = Constant(2.0)*Circumradius(mesh)
alpha = Constant(1)
gamma = Constant(1)
n = FacetNormal(mesh)
a = inner(grad(u), grad(v))*dx \
- dot(avg(grad(u)), jump(v, n))*dS \
- dot(jump(u, n), avg(grad(v)))*dS \
+ alpha/avg(h)*dot(jump(u, n), jump(v, n))*dS \
- dot(grad(u), v*n)*ds \
- dot(u*n, grad(v))*ds \
+ gamma/h*u*v*ds
L = f*v*dx
u_h = Function(DG1, name='u_h')
bc = DirichletBC(DG1, 0, 'on_boundary')
solve(a == L, u_h, bcs=bc)
fig, ax = plt.subplots(figsize=[8, 4], subplot_kw=dict(projection='3d'))
ts = trisurf(u_h, axes=ax)
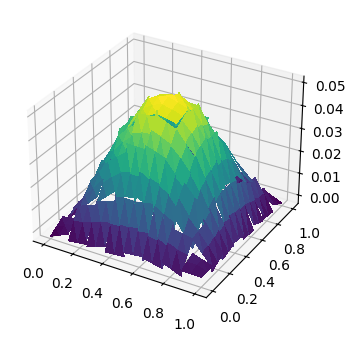
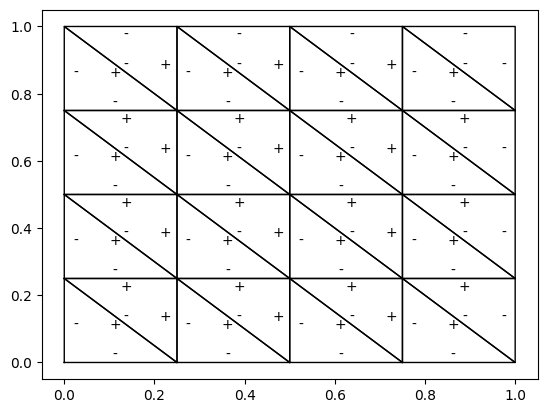
2.2.4. Positive and negative part of inner boundary#
from firedrake import *
from firedrake.petsc import PETSc
import os, sys
import numpy as np
import matplotlib.pyplot as plt
# plt.rcParams.update({'font.size': 14})
N = PETSc.Options().getInt('N', default=4)
m = RectangleMesh(N, N, 1, 1)
V = FunctionSpace(m, 'DG', 0)
Vc = VectorFunctionSpace(m, 'DG', 0)
V_e = FunctionSpace(m, 'HDivT', 0)
V_ec = VectorFunctionSpace(m, 'HDivT', 0)
x, y = SpatialCoordinate(m)
u = Function(V, name='u')
uc = Function(Vc).interpolate(m.coordinates)
u_e = Function(V_e, name='u_e')
u_ec = Function(V_ec).interpolate(m.coordinates)
ncell = len(u.dat.data_ro)
factor = 0.7
for i in range(ncell):
cell = V.cell_node_list[i][0]
u.dat.data_with_halos[:] = 0
u.dat.data_with_halos[cell] = 1
es = V_e.cell_node_list[i]
cc = uc.dat.data_ro_with_halos[cell, :]
vertex = m.coordinates.dat.data_ro_with_halos[
m.coordinates.function_space().cell_node_list[i]
]
vertex = np.vstack([vertex, vertex[0]])
plt.plot(vertex[:, 0], vertex[:, 1], 'k', lw=1)
for e in es:
u_e.dat.data_with_halos[:] = 0
u_e.dat.data_with_halos[e] = 1
ec = u_ec.dat.data_ro_with_halos[e, :]
dis = ec - cc
v_p, v_m = assemble(u('+')*u_e('+')*dS), assemble(u('-')*u_e('-')*dS)
_x = cc[0] + factor*dis[0]
_y = cc[1] + factor*dis[1]
plt.text(_x, _y, '+' if v_p > 0 else '-', ha='center', va='center')
rank, size = m.comm.rank, m.comm.size
if not os.path.exists('figures'):
os.makedirs('figures')
plt.savefig(f'figures/dgflag_{size}-{rank}.pdf')
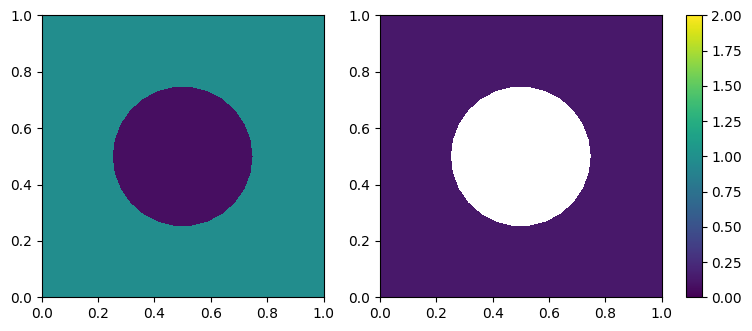
2.3. 指示函数#
from firedrake import *
from firedrake.pyplot import triplot, tricontourf
import matplotlib.pyplot as plt
# set marker function by solving equation
def make_marker_solve_equ(mesh, tag, value=1):
V = FunctionSpace(mesh, 'DG', 0)
u, v = TrialFunction(V), TestFunction(V)
f = Function(V)
solve(u*v*dx == Constant(value)*v*dx(tag) + Constant(0)*v*dx, f)
return f
# set marker function by using par_loop
def make_marker_par_loop(mesh, tag, value=1):
V = FunctionSpace(mesh, 'DG', 0)
f = Function(V)
domain = '{[i]: 0 <= i < A.dofs}'
instructions = '''
for i
A[i] = {value}
end
'''
# par_loop((domain, instructions.format(value=0)), dx, {'A' : (f, WRITE)})
par_loop((domain, instructions.format(value=value)), dx(tag), {'A' : (f, WRITE)})
return f
mesh = Mesh('gmsh/circle_in_rect.msh')
f1 = make_marker_solve_equ(mesh, tag=1, value=1)
f2 = make_marker_par_loop(mesh, tag=2, value=2)
np.allclose(f1.dat.data, f2.dat.data)
False
from matplotlib import cm
from matplotlib import colormaps
from matplotlib.colors import Normalize
cmap = colormaps.get_cmap('viridis')
normalizer = Normalize(0, 2)
smap = cm.ScalarMappable(norm=normalizer, cmap=cmap)
fig, axes = plt.subplots(1, 2, figsize=[8, 4])
axes[0].set_aspect('equal')
axes[1].set_aspect('equal')
cs0 = tricontourf(f1, axes=axes[0], cmap=cmap, norm=normalizer)
cs1 = tricontourf(f2, axes=axes[1], cmap=cmap, norm=normalizer)
# fig.colorbar(smap, ax=axes.ravel().tolist())
pos = axes[1].get_position()
cax = fig.add_axes([pos.x1 + 0.03, pos.y0, 0.02, pos.height])
fig.colorbar(smap, cax=cax)
<matplotlib.colorbar.Colorbar at 0x7f95c2c45820>
from firedrake import *
from firedrake.pyplot import tricontourf
import matplotlib.pyplot as plt
mesh = RectangleMesh(2, 2, 1, 1)
V = FunctionSpace(mesh, 'DG', 0)
f = Function(V)
f.dat.data[:] = -2
f.dat.data[0:2] = 0
tricontourf(f)
<matplotlib.tri._tricontour.TriContourSet at 0x7f95d02c1c10>
2.4. Dirac Delta 函数#
2.4.1. 通过数值积分公式实现 dirac delta 函数#
from firedrake import *
from firedrake.petsc import PETSc
from pyop2 import op2
from pyop2.datatypes import ScalarType
from mpi4py import MPI
import finat
import numpy as np
import matplotlib.pyplot as plt
set_level(CRITICAL) # Disbale warnings
class DiracOperator(object):
def __init__(self, m, x0):
"""Make Dirac delta operator at point
Args:
m: mesh
x0: source point
Example:
delta = DiracOperator(m, x0)
f = Function(V)
f_x0 = assemble(delta(f))
"""
self.mesh = m
self.x0 = x0
self.operator = None
def __call__(self, f):
if self.operator is None:
self._init()
return self.operator(f)
def _init(self):
m = self.mesh
x0 = self.x0
V = FunctionSpace(m, 'DG', 0)
cell_marker = Function(V, name='cell_marker', dtype=ScalarType)
qrule = finat.quadrature.make_quadrature(V.finat_element.cell, 0)
cell, X = m.locate_cell_and_reference_coordinate(x0, tolerance=1e-6)
# c = 0 if X is None else 1
n_cell_local = len(cell_marker.dat.data)
if X is not None and cell < n_cell_local:
c = 1
else:
c = 0
comm = m.comm
s = comm.size - comm.rank
n = comm.allreduce(int(s*c), op=MPI.MAX)
if n == 0:
raise BaseException("Points not found!")
k = int(comm.size - n) # get the lower rank which include the point x0
if c == 1 and comm.rank == k:
X[X<0] = 0
X[X>1] = 1
cell_marker.dat.data[cell] = 1
comm.bcast(X, root=k)
else:
cell_marker.dat.data[:] = 0 # we must set this otherwise the process will hangup
X = comm.bcast(None, root=k)
cell_marker.dat.global_to_local_begin(op2.READ)
cell_marker.dat.global_to_local_end(op2.READ)
qrule.point_set.points[0] = X
qrule.weights[0] = qrule.weights[0]/np.real(assemble(cell_marker*dx))
self.operator = lambda f: f*cell_marker*dx(scheme=qrule)
2.4.2. 测试 DiracOperator#
def test_dirca_delta_1D():
test_mesh = IntervalMesh(8, 1)
V = FunctionSpace(test_mesh, 'CG', 3)
x1 = 0.683
source = Constant([x1,])
delta = DiracOperator(test_mesh, source)
x, = SpatialCoordinate(test_mesh)
g = Function(V).interpolate(x**2)
expected_value = g.at([x1])
value = assemble(delta(g))
PETSc.Sys.Print(f"value = {value}, expected value = {expected_value}")
test_dirca_delta_1D()
/opt/firedrake/firedrake/function.py:560: FutureWarning: The ``Function.at`` method is deprecated and will be removed in a future release. Please use the ``PointEvaluator`` class instead.
warnings.warn(
/usr/local/lib/python3.12/dist-packages/ufl/utils/sorting.py:94: UserWarning: Applying str() to a metadata value of type QuadratureRule, don't know if this is safe.
warnings.warn(
value = 0.46648900000000015, expected value = 0.4664889999999999
def test_dirca_delta_2D():
test_mesh = RectangleMesh(8, 8, 1, 1)
V = FunctionSpace(test_mesh, 'CG', 3)
x1 = 0.683
x2 = 0.333
source = Constant([x1,x2])
x0 = source
delta = DiracOperator(test_mesh, source)
x, y = SpatialCoordinate(test_mesh)
g = Function(V).interpolate(x**3 + y**3)
expected_value = g.at([x1, x2])
value = assemble(delta(g))
PETSc.Sys.Print(f"value = {value}, expected value = {expected_value}")
test_dirca_delta_2D()
/opt/firedrake/firedrake/function.py:560: FutureWarning: The ``Function.at`` method is deprecated and will be removed in a future release. Please use the ``PointEvaluator`` class instead.
warnings.warn(
/usr/local/lib/python3.12/dist-packages/ufl/utils/sorting.py:94: UserWarning: Applying str() to a metadata value of type QuadratureRule, don't know if this is safe.
warnings.warn(
value = 0.35553802400000006, expected value = 0.35553802400000023
2.4.3. Dirac delta 函数的 L2 投影#
test_mesh = RectangleMesh(10, 10, 1, 1)
V = FunctionSpace(test_mesh, 'CG', 3)
delta = DiracOperator(test_mesh, [0.638, 0.33])
bc = DirichletBC(V, 0, 'on_boundary')
u, v = TrialFunction(V), TestFunction(V)
sol = Function(V)
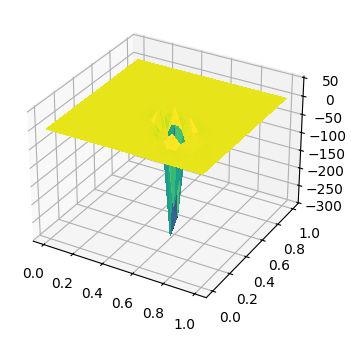
solve(u*conj(v)*dx == delta(conj(v)), sol, bcs=bc)
fig, ax = plt.subplots(figsize=[8, 4], subplot_kw=dict(projection='3d'))
ts = trisurf(sol, axes=ax) # 为什么负值那么大?
/usr/local/lib/python3.12/dist-packages/ufl/utils/sorting.py:94: UserWarning: Applying str() to a metadata value of type QuadratureRule, don't know if this is safe.
warnings.warn(
2.4.4. 求解源项为 Dirca delta 函数的 Possion 方程#
x0 = [0, 0]
# N = 500
# m = SquareMesh(N, N, 1)
m = UnitDiskMesh(refinement_level=3)
V = FunctionSpace(m, 'CG', 1)
v = TestFunction(V)
u = TrialFunction(V)
a = inner(grad(u), grad(v))*dx
L = DiracOperator(m, x0)(v)
u = Function(V, name='u')
bc = DirichletBC(V, 0, 'on_boundary')
solve(a == L, u, bcs=bc)
# solve(a == L, u)
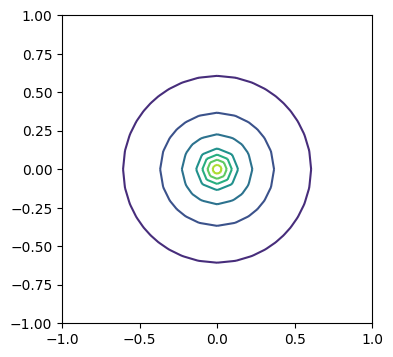
fig, ax = plt.subplots(figsize=[4, 4])
ts = tricontour(u, axes=ax)
/usr/local/lib/python3.12/dist-packages/ufl/utils/sorting.py:94: UserWarning: Applying str() to a metadata value of type QuadratureRule, don't know if this is safe.
warnings.warn(
2.5. 变分求解器中修改 Jacobian 和残差的接口(回调函数)#
Firedrake 使用 PETSc 的 SNES 对非线性问题 (包括线性问题)
进行求解,并提供了4个回调函数 pre_jacobian_callback, post_jacobian_callback, pre_function_callback, post_function_callback.
用于在组装前后修改 Jacobian ( \(J = F'(x)\) ) 和残差 \(F(x)\).
代码示例见”定义 Solver”.
2.6. 自由度映射关系#
2.6.1. Cell node map#
V.dim(): Number of dofsV.cell_node_list: an array of cell node map (same withV.cell_node_map().values)
mesh = RectangleMesh(8, 8, 1, 1)
V = FunctionSpace(mesh, 'CG', 1)
# the global numers of the dofs in the first 2 elements
for i in range(2):
print(f"cell {i}: ", V.cell_node_list[i])
cell 0: [0 1 2]
cell 1: [1 2 3]
Example: 第一个三角形的坐标
coords = mesh.coordinates
V_c = coords.function_space()
dof_numbers = V_c.cell_node_list[0]
for i in dof_numbers:
print(f"vertex {i}:", coords.dat.data_ro_with_halos[i])
vertex 0: [0. 0.]
vertex 1: [0. 0.125]
vertex 2: [0.125 0. ]
2.6.2. Finite element (dofs on reference cell)#
V = FunctionSpace(mesh, 'CG', 2)
element = V.finat_element
print("cell: ", element.cell)
print("degree: ", element.degree)
cell: UFCTriangle(2, ((0.0, 0.0), (1.0, 0.0), (0.0, 1.0)), {0: {0: (0,), 1: (1,), 2: (2,)}, 1: {0: (1, 2), 1: (0, 2), 2: (0, 1)}, 2: {0: (0, 1, 2)}})
degree: 2
element.entity_dofs() # dofs for every entity (vertex, edge, face, volume)
{0: {0: [0], 1: [3], 2: [5]}, 1: {2: [1], 1: [2], 0: [4]}, 2: {0: []}}
参考单元中几何实体 (Entity) 的连接关系参考代码:
详细的介绍可以参考 [ALM12].
2.7. par_loop 的使用#
help(par_loop)
2.7.1. 计算四面体面的外接圆半径#
def get_facet_circumradius_3d(mesh):
V0 = FunctionSpace(mesh, 'HDivT', 0)
facet_circumradius = Function(V0)
domain = '{[i]: 0 <= i < A.dofs}'
instructions = '''
for i
<> j0 = (i+1)%4
<> j1 = (i+2)%4
<> j2 = (i+3)%4
<> u0 = B[j1,0] - B[j0,0]
<> u1 = B[j1,1] - B[j0,1]
<> u2 = B[j1,2] - B[j0,2]
<> v0 = B[j2,0] - B[j0,0]
<> v1 = B[j2,1] - B[j0,1]
<> v2 = B[j2,2] - B[j0,2]
<> S = sqrt(pow(u1*v2 - u2*v1, 2.) + pow(u2*v0 - u0*v2, 2.) + pow(u0*v1 - u1*v0, 2.))/2
<> a = sqrt(pow(u0, 2.) + pow(u1, 2.) + pow(u2, 2.))
<> b = sqrt(pow(v0, 2.) + pow(v1, 2.) + pow(v2, 2.))
<> c = sqrt(pow(u0 - v0, 2.) + pow(u1 - v1, 2.) + pow(u2 - v2, 2.))
A[i] = a*b*c/(4*S)
end
'''
par_loop((domain, instructions), dx,
{'A': (facet_circumradius, WRITE), 'B' :(mesh.coordinates, READ)})
return facet_circumradius
mesh = UnitCubeMesh(1, 1, 1)
facet_R = get_facet_circumradius_3d(mesh)
facet_R.dat.data[facet_R.function_space().cell_node_list]
array([[0.70710678, 0.8660254 , 0.8660254 , 0.70710678],
[0.70710678, 0.8660254 , 0.70710678, 0.8660254 ],
[0.70710678, 0.8660254 , 0.70710678, 0.8660254 ],
[0.70710678, 0.70710678, 0.8660254 , 0.8660254 ],
[0.70710678, 0.70710678, 0.8660254 , 0.8660254 ],
[0.70710678, 0.70710678, 0.8660254 , 0.8660254 ]])
2.7.2. 计算四面体面的重心#
def get_facet_center_3d(mesh):
V0 = VectorFunctionSpace(mesh, 'HDivT', 0)
facet_center = Function(V0)
domain = '{[i]: 0 <= i < A.dofs}'
instructions = '''
for i
<> j0 = (i+1)%4
<> j1 = (i+2)%4
<> j2 = (i+3)%4
A[i, 0] = (B[j0, 0] + B[j1, 0] + B[j2, 0])/3
A[i, 1] = (B[j0, 1] + B[j1, 1] + B[j2, 1])/3
A[i, 2] = (B[j0, 2] + B[j1, 2] + B[j2, 2])/3
end
'''
par_loop((domain, instructions), dx,
{'A': (facet_center, WRITE), 'B' :(mesh.coordinates, READ)})
return facet_center
测试重心是否计算正确 (和插值做对比)
mesh = UnitCubeMesh(1, 1, 1)
facet_center = get_facet_center_3d(mesh)
V0 = VectorFunctionSpace(mesh, 'HDivT', 0)
facet_center2 = Function(V0).interpolate(mesh.coordinates)
assert np.allclose(facet_center.dat.data - facet_center2.dat.data, 0)
2.8. Adaptive Finite Element Methods#
2.8.1. Possion on Lshape#
File: py/adapt_possion.py
方程求解
def solve_possion(mesh, u_handle, f_handle): x = SpatialCoordinate(mesh) u_e = u_handle(x) f = f_handle(x) V = FunctionSpace(mesh, 'CG', 1) u, v = TrialFunction(V), TestFunction(V) L = inner(f, v)*dx a = inner(grad(u), grad(v))*dx sol = Function(V, name='u_h') bc = DirichletBC(V, u_e, 'on_boundary') solve(a == L, sol, bcs=bc) err = errornorm(u_e, sol, norm_type='H1')/norm(u_e, norm_type='H1') return sol, err
误差估计
def estimate(mesh, sol, u_handle, f_handle, alpha, beta): x = SpatialCoordinate(mesh) u_e = u_handle(x) f = f_handle(x) V_eta_K = FunctionSpace(mesh, 'DG', 0) V_eta_e = FunctionSpace(mesh, 'HDivT', 0) phi_K = TestFunction(V_eta_K) phi_e = TestFunction(V_eta_e) phi = div(grad(sol)) + f g = jump(grad(sol), FacetNormal(mesh)) ksi_K = assemble(inner(phi**2, phi_K)*dx) ksi_e = assemble(inner(g**2, avg(phi_e))*dS) ksi_outer = assemble(inner((sol-u_e)**2, phi_e)*ds) h_e = assemble(conj(phi_e)*ds) h_K = Function(V_eta_K).interpolate(CellDiameter(mesh)) eta_K = assemble_eta_K_op2(ksi_K, ksi_e, ksi_outer, h_K, h_e, alpha=alpha, beta=beta) # eta_K2 = assemble_eta_K_py(ksi_K, ksi_e, ksi_outer, h_K, h_e, alpha=alpha, beta=beta) # assert np.allclose(eta_K.dat.data_ro_with_halos, eta_K2.dat.data_ro_with_halos) return eta_K
def assemble_eta_K_py(ksi_K, ksi_e, ksi_outer, h_K, h_e, alpha, beta): V_eta_K = ksi_K.function_space() V_eta_e = ksi_e.function_space() cell_node_list_K = V_eta_K.cell_node_list cell_node_list_e = V_eta_e.cell_node_list ne_per_cell = V_eta_e.cell_node_list.shape[1] s1 = np.zeros_like(ksi_K.dat.data_ro_with_halos) for i in range(0, ne_per_cell): s1 += ksi_e.dat.data_ro_with_halos[cell_node_list_e[:, i]] s2 = np.zeros_like(ksi_K.dat.data_ro_with_halos) for i in range(0, ne_per_cell): s2 += h_e.dat.data_ro_with_halos[cell_node_list_e[:, i]] * ksi_outer.dat.data_ro_with_halos[cell_node_list_e[:, i]] eta_K = Function(V_eta_K) eta_K.dat.data_with_halos[:] = np.sqrt( alpha * h_K.dat.data_ro_with_halos**2 * ksi_K.dat.data_ro_with_halos \ + beta * h_K.dat.data_ro_with_halos * s1 # + beta * (h_K.dat.data_ro_with_halos * s1 + s2) ) return eta_K
网格标记
def mark_cells(mesh, eta_K, theta): plex = mesh.topology_dm cell_numbering = mesh._cell_numbering if plex.hasLabel('adapt'): plex.removeLabel('adapt') with eta_K.dat.vec_ro as vec: eta = vec.norm() eta_max = vec.max()[1] cell_node_list_K = eta_K.function_space().cell_node_list tol = theta*eta_max eta_K_data = eta_K.dat.data_ro_with_halos with PETSc.Log.Event("ADD_ADAPT_LABEL"): plex.createLabel('adapt') cs, ce = plex.getHeightStratum(0) for i in range(cs, ce): c = cell_numbering.getOffset(i) dof = cell_node_list_K[c][0] if eta_K_data[dof] > tol: plex.setLabelValue('adapt', i, 1) return plex
使用以上函数以及 DMPlex 的 adaptLabel 方法, 我们可以写出 L 区域上的网格自适应方法
def adapt_possion_Lshape():
om = OptionsManager({"dm_plex_transform_type": "refine_sbr"}, options_prefix='')
def u_exact(x):
mesh = x.ufl_domain()
U = FunctionSpace(mesh, 'CG', 1)
u = Function(U)
coords = mesh.coordinates
x1, x2 = np.real(coords.dat.data_ro[:, 0]), np.real(coords.dat.data_ro[:, 1])
r = np.sqrt(x1**2 + x2**2)
theta = np.arctan2(x2, x1)
u.dat.data[:] = r**(2/3)*np.sin(2*theta/3)
return u
def f_handle(x):
return Constant(0)
mesh = Mesh('gmsh/Lshape.msh')
result = []
parameters = {}
parameters["partition"] = False
for i in range(10):
if i != 0:
eta_K = estimate(mesh, sol, u_exact, f_handle, alpha=0.15, beta=0.15)
plex = mark_cells(mesh, eta_K, theta=0.2)
with PETSc.Log.Event("ADAPT"):
with om.inserted_options():
new_plex = plex.adaptLabel('adapt')
# Remove labels to avoid errors
new_plex.removeLabel('adapt')
remove_pyop2_label(new_plex)
new_plex.viewFromOptions('-dm_view')
# mesh = Mesh(new_plex, distribution_parameters=parameters)
mesh = Mesh(new_plex)
sol, err = solve_possion(mesh, u_exact, f_handle)
ndofs = sol.function_space().dim()
result.append((ndofs, np.real(err)))
return result
2.8.2. L 型区域上的网格自适应算例#
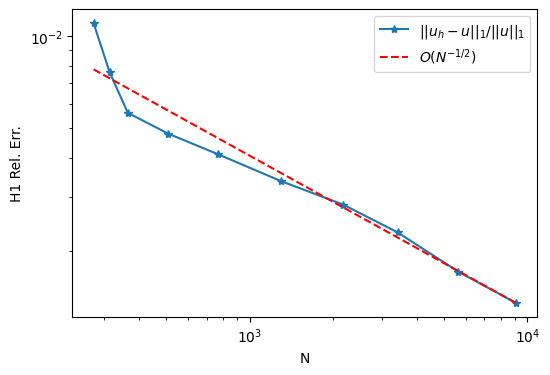
from py.adapt_possion import adapt_possion_Lshape, plot_adapt_result
result = adapt_possion_Lshape()
fig = plot_adapt_result(result)
2.8.3. Update coordinates of DMPlex#
File: py/update_plex_coordinates.py
如果移动了网格, DMPlex 中存储的坐标和 Firedrake 的坐标将会不一致, 这时候做自适应加密需要把同步 Firedrake 中的坐标 DMPlex 中.
根据自由度的映射关系, 更新
plex的坐标.def get_plex_with_update_coordinates(mesh: MeshGeometry): """ Update the coordinates of the plex in mesh, and then return a clone without pyop2 label """ if hasattr(mesh.topology, 'init'): mesh.topology.init() dm = mesh.topology_dm.clone() csec = dm.getCoordinateSection() coords_vec = dm.getCoordinatesLocal() s, e = dm.getDepthStratum(0) sec = mesh._vertex_numbering data = mesh.coordinates.dat.data_ro_with_halos dest = np.zeros_like(data) n = mesh.geometric_dimension() m = csec.getFieldComponents(0) assert m == n for i in range(s, e): # dof = sec.getDof(i) offset = sec.getOffset(i) # cdof = csec.getDof(i) coffset = csec.getOffset(i) dest[coffset//m] = data[offset, :] coords_vec.array_w[:] = dest.flatten() # dm.setCoordinatesLocal(coords_vec) remove_pyop2_label(dm) return dm
通过设置
Section的方式更新plex.若使用的 Firedrake 包含 pr-2933, 则可以使用该方式.
def get_plex_with_update_coordinates_new(mesh: MeshGeometry): tdim = mesh.topological_dimension() gdim = mesh.geometric_dimension() entity_dofs = np.zeros(tdim + 1, dtype=np.int32) entity_dofs[0] = gdim coord_section = mesh.create_section(entity_dofs) plex = mesh.topology_dm.clone() coord_dm = plex.getCoordinateDM() coord_dm.setSection(coord_section) coords_local = coord_dm.createLocalVec() coords_local.array[:] = np.reshape( mesh.coordinates.dat.data_ro_with_halos, coords_local.array.shape ) plex.setCoordinatesLocal(coords_local) remove_pyop2_label(plex) return plex
Warning
对于不包含 pr-2933 的版本, 上述方法虽然可以更新坐标, 但是更新后的
plex不可以作为Mesh的参数创建网格.
使用移动网格进行测试
from firedrake import *
from py.update_plex_coordinates import \
get_plex_with_update_coordinates, \
get_plex_with_update_coordinates_new
import matplotlib.pyplot as plt
def save_mesh(mesh, name):
V = FunctionSpace(mesh, 'CG', 1)
f = Function(V, name='f')
File(name).write(f)
mesh_init = RectangleMesh(5, 5, 1, 1)
# move mesh
mesh_init.coordinates.dat.data[:] += 1
save_mesh(mesh_init, 'pvd/mesh_init.pvd')
# recreate mesh from the plex
plex = get_plex_with_update_coordinates(mesh_init)
mesh = Mesh(plex, distribution_parameters={"partition": False})
save_mesh(mesh, 'pvd/mesh_with_update_plex.pvd')
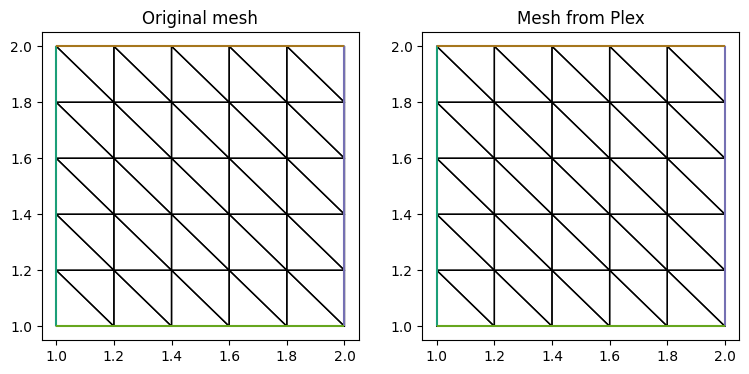
fig, ax = plt.subplots(1, 2, figsize=[9, 4], subplot_kw={})
tp0 = triplot(mesh_init, axes=ax[0])
tp1 = triplot(mesh, axes=ax[1])
t0 = ax[0].set_title('Original mesh')
t1 = ax[1].set_title('Mesh from Plex')
/opt/firedrake/firedrake/_deprecation.py:65: UserWarning: The use of `File` for output is deprecated, please update your code to use `VTKFile` from `firedrake.output`.
warn(
/opt/firedrake/firedrake/_deprecation.py:65: UserWarning: The use of `File` for output is deprecated, please update your code to use `VTKFile` from `firedrake.output`.
warn(
2.8.4. Using adaptMetric of dmplex#
除了上述 adaptLabel 方法, PETSc 还提供的 adaptMetric 方法根据用户
提供的度量矩阵对网格进行自适应. 该度量矩阵是 PETSc 的 LocalVector.
首先使用 create_metric_from_indicator 把 indicator 转化为度量矩阵 v, 然后使用 to_petsc_local_numbering 把自由度排序更改为 PETSc 内部序. 注意这里网格每个节点对应一个度量矩阵, 用向量表示.
最后调用 adaptMetric 进行自适应网格剖分.
def adapt(indicator):
mesh = indicator.ufl_domain()
metric = create_metric_from_indicator(indicator)
v = PETSc.Vec().createWithArray(metric.dat._data,
size=(metric.dat._data.size, None),
bsize=metric.dat.cdim, comm=metric.comm)
reordered = to_petsc_local_numbering_for_local_vec(v, metric.function_space())
v.destroy()
plex_new = mesh.topology_dm.adaptMetric(reordered, "Face Sets", "Cell Sets")
mesh_new = Mesh(plex_new)
return mesh_new
方法 create_metric_from_indicator 根据输入参数构造度量矩阵, 其思路为先计算各单元的度量矩阵, 然后顶点的度量矩阵通过相邻单元的度量矩阵进行加权平均得到
对单元循环, 求解单元度量矩阵
82 for j in range(i): 83 pair.append([i, j]) 84 85 for k, nodes in enumerate(Vc.cell_node_list): 86 vertex = coords[nodes, :] 87 edge = [] 88 for i, j in pair: 89 edge.append(vertex[i, :] - vertex[j, :])
这里用到了
edge2vec用于根据单元边向量构造计算度量矩阵的矩阵67 ind = indicator.dat.data_with_halos 68 69 dim = mesh.geometric_dimension() 70 71 if dim == 2: 72 edge2vec = lambda e: [ e[0]**2, 2*e[0]*e[1], e[1]**2 ] 73 vec2tensor = lambda g: [[g[0], g[1]], [g[1], g[2]]] 74 elif dim == 3:
根据单元体积进行加权平均, 计算顶点的度量矩阵
91 mat = [] 92 for e in edge: 93 mat.append(edge2vec(e)) 94 95 mat = np.array(mat) 96 b = np.ones(len(edge)) 97 g = np.linalg.solve(mat, b)
方法 to_petsc_local_numbering_for_local_vec 内容如下
def to_petsc_local_numbering_for_local_vec(vec, V):
section = V.dm.getLocalSection()
out = vec.duplicate()
varray = vec.array_r
oarray = out.array
dim = V.value_size
idx = 0
for p in range(*section.getChart()):
dof = section.getDof(p)
off = section.getOffset(p)
# PETSc.Sys.syncPrint(f"dof = {dof}, offset = {off}")
if dof > 0:
off = section.getOffset(p)
off *= dim
for d in range(dof):
for k in range(dim):
oarray[idx] = varray[off + dim * d + k]
idx += 1
# PETSc.Sys.syncFlush()
return out
通过命令行选项或 OptionsManager, 我们可以控制使用的自适应库 pragmatic, mmg, parmmg.
def test_adapt(dim=2, factor=2):
if dim == 2:
mesh = UnitSquareMesh(5, 5)
elif dim == 3:
mesh = UnitCubeMesh(5, 5, 5)
else:
raise Exception("")
V = FunctionSpace(mesh, 'DG', 0)
indicator = Function(V, name='indicator')
indicator.dat.data[:] = factor
mesh_adapt = adapt(indicator)
mesh.topology_dm.viewFromOptions('-dm_view')
mesh_adapt.topology_dm.viewFromOptions('-dm_view_new')
return mesh, mesh_adapt
def test_adapt_with_option(dim=2, factor=0.5, adaptor=None):
# adaptors: pragmatic, mmg, parmmg
# -dm_adaptor pragmatic
# -dm_adaptor mmg # 2d or 3d (seq)
# -dm_adaptor parmmg # 3d (parallel)
adaptors = get_avaiable_adaptors()
if adaptors is None:
PETSc.Sys.Print("No adaptor found. You need to install pragmatic, mmg, or parmmg with petsc.")
return None
if adaptor is not None and adaptor not in adaptors:
PETSc.Sys.Print(f"Adaptor {adaptor} not installed with petsc. Installed adaptors: {adaptors}.")
return None
if adaptor is None:
adaptor = adaptors[0]
parameters = {
"dm_adaptor": adaptor,
# "dm_plex_metric_target_complexity": 400,
# "dm_view": None,
# "dm_view_new": None,
}
om = OptionsManager(parameters, options_prefix="")
with om.inserted_options():
mesh, mesh_new = test_adapt(dim=dim, factor=factor)
return mesh, mesh_new
下面我们展示一个三维立方体区域自适应的结果
from py.test_adapt_metric import test_adapt, test_adapt_with_option
from firedrake import triplot
import matplotlib.pyplot as plt
# adaptor: pragmatic, mmg, parmmg
# pragmatic, mmg, parmmg not installed in firedrake offcial docker image
ret = test_adapt_with_option(dim=3, factor=.3, adaptor="mmg")
if ret is not None:
mesh, mesh_new = ret
if mesh.geometric_dimension() == 3:
subplot_kw = dict(projection='3d')
else:
subplot_kw = {}
fig, ax = plt.subplots(1, 2, figsize=[9, 4], subplot_kw=subplot_kw)
tp = triplot(mesh, axes=ax[0])
tp_new = triplot(mesh_new, axes=ax[1])
t0 = ax[0].set_title('Original mesh')
t1 = ax[1].set_title('Adapted mesh')
No adaptor found. You need to install pragmatic, mmg, or parmmg with petsc.
/opt/firedrake/firedrake/utils.py:167: FutureWarning: get_external_packages is deprecated and will be removed, please use petsctools.get_external_packages instead
warnings.warn(msg, warning_type)
2.9. 使用 DM.adaptLabel 进行网格加密#
from firedrake import RectangleMesh, Mesh, triplot
# load original mesh
mesh = RectangleMesh(4, 4, 1, 1)
c = triplot(mesh)
plex = mesh.topology_dm
# # or just read from gmsh file
# comm = COMM_WORLD
# plex = PETSc.DMPlex().createFromFile('mymesh.msh', comm)

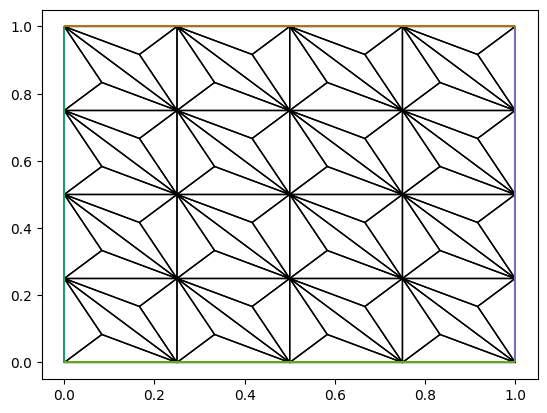
PETSc 中的 DMPlex 类提供了用于网格变换的功能, 参考 Summary of Unstructured Mesh Transformations. 下面是网格重心加密的示例.
# Barycentric refinement for simplicies
# https://petsc.org/main/overview/plex_transform_table/
# opts = PETSc.Options()
# opts.insertString('-dm_plex_transform_type refine_alfeld') # can be set in command line
try:
from petsctools.options import OptionsManager
except ImportError:
from firedrake.petsc import OptionsManager
om = OptionsManager({"dm_plex_transform_type": "refine_alfeld"}, options_prefix='')
with om.inserted_options():
new_plex = plex.adaptLabel(None)
new_mesh = Mesh(new_plex)
c = triplot(new_mesh)
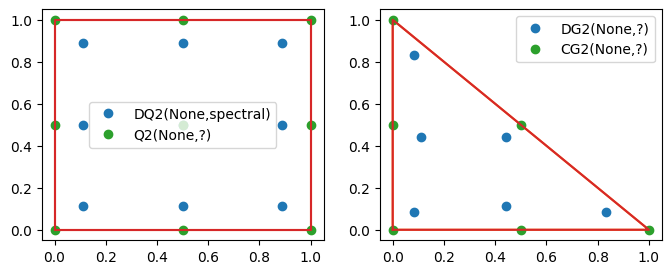
2.10. Examples on the variant parameter for FiniteElement#
from firedrake import *
import ufl
import numpy as np
import matplotlib.pyplot as plt
from scipy.spatial import ConvexHull
def show_dofs(V, ax=None):
"""Show the position of the nodes in the dual space"""
if ax is None:
fig, ax = plt.subplots(figsize=[4, 3])
ele = V.ufl_element()
ps = V.finat_element.dual_basis[1]
ax.plot(ps.points[:, 0], ps.points[:, 1], 'o', label=ele.shortstr())
cell = V.finat_element.cell
vertices = np.array(cell.get_vertices())
hull = ConvexHull(vertices)
index = list(hull.vertices)
index.append(index[0])
ax.plot(vertices[index, 0], vertices[index, 1])
ax.legend() # (bbox_to_anchor=(1, 1))
return ax
p = 2 # or set to 3 to make it clear
# https://www.firedrakeproject.org/variational-problems.html#id14
# fe = FiniteElement("DQ", mesh.ufl_cell(), p, variant="equispaced")
mesh = RectangleMesh(1, 1, 1, 1, quadrilateral=True)
fe = FiniteElement("DQ", mesh.ufl_cell(), p, variant="spectral") # default
V1 = FunctionSpace(mesh, fe)
V2 = FunctionSpace(mesh, 'CG', p)
fig, ax = plt.subplots(1, 2, figsize=[8, 3])
show_dofs(V1, ax=ax[0])
show_dofs(V2, ax=ax[0])
mesh = RectangleMesh(1, 1, 1, 1, quadrilateral=False)
V1 = FunctionSpace(mesh, 'DG', p)
V2 = FunctionSpace(mesh, 'CG', p)
show_dofs(V1, ax=ax[1])
show_dofs(V2, ax=ax[1])
<Axes: >
2.11. Interpolation errors for highly oscillating functions#
The linear interpolation error of functions with wave number \(k\) is
from firedrake import *
import numpy as np
import matplotlib.pyplot as plt
def get_H1_expr(e):
return (inner(e, e) + inner(grad(e), grad(e)))*dx
N = 64
mesh = RectangleMesh(N, N, 1, 1)
h = 1/N
x = SpatialCoordinate(mesh)
k = Constant(1)
f = cos(k*sqrt(dot(x,x)))
p = 1
V = FunctionSpace(mesh, 'CG', p)
V_ref = FunctionSpace(mesh, 'CG', p+2)
Int = Interpolator(f, V)
Int_ref = Interpolator(f, V_ref)
f_int = Function(V)
f_ref = Function(V_ref)
e = f_int - f
e_ref = f_int - f_ref
f_H1 = get_H1_expr(f)
f_ref_H1 = get_H1_expr(f_ref)
f_int_H1 = get_H1_expr(f_int)
e_H1 = get_H1_expr(e)
e_ref_H1 = get_H1_expr(e_ref)
ks = np.linspace(0, 1000, 200)
errors = np.zeros((len(ks), 2))
dtype = np.dtype([
('k', 'f8'),
('f_H1', 'f8'),
('f_ref_H1', 'f8'),
('f_int_H1', 'f8'),
('e_H1', 'f8'),
('e_ref_H1', 'f8'),
])
ret = np.zeros(len(ks), dtype=dtype)
for i, _k in enumerate(ks):
k.assign(_k)
Int.interpolate(output=f_int)
Int_ref.interpolate(output=f_ref)
a = sqrt(assemble(f_H1)), sqrt(assemble(f_ref_H1)), sqrt(assemble(f_int_H1))
b = sqrt(assemble(e_H1)), sqrt(assemble(e_ref_H1))
ret[i] = (_k, *a, *b)
---------------------------------------------------------------------------
TypeError Traceback (most recent call last)
Cell In[29], line 51
49 for i, _k in enumerate(ks):
50 k.assign(_k)
---> 51 Int.interpolate(output=f_int)
52 Int_ref.interpolate(output=f_ref)
53 a = sqrt(assemble(f_H1)), sqrt(assemble(f_ref_H1)), sqrt(assemble(f_int_H1))
TypeError: Interpolator.interpolate() got an unexpected keyword argument 'output'
fig, axes = plt.subplots(1, 2, figsize=[10, 3])
e_H1_rel = ret['e_H1']/ret['f_H1']
e_ref_H1_rel = ret['e_ref_H1']/ret['f_H1']
axes[0].plot(ret['k'], e_H1_rel, label='$I_h f - f$')
axes[0].plot(ret['k'], e_ref_H1_rel, label='$I_h f - f_{ref}$')
ref_line = e_H1_rel[10]*ret['k']/ret['k'][10]
ref_line[ref_line>1] = 1
axes[0].plot(ret['k'], ref_line, ':', label='$O(k)$')
upper = max(e_H1_rel.max(), e_ref_H1_rel.max())
for n in (1, 5):
k_max = 2*pi/(n*h)
axes[0].plot([k_max, k_max], [0, upper], 'b--')
axes[0].set_xlabel('$k$')
axes[0].set_ylabel('Relatively $H1$-Error')
axes[0].legend()
axes[1].plot(ret['k'], ret['e_H1'], label='$I_h f - f$')
axes[1].plot(ret['k'], ret['e_ref_H1'], label='$I_h f - f_{ref}$')
upper = max(ret['e_H1'].max(), ret['e_ref_H1'].max())
for n in (1, 5):
k_max = 2*pi/(n*h)
axes[1].plot([k_max, k_max], [0, upper], 'b--')
axes[1].set_xlabel('$k$')
axes[1].set_ylabel('$H1$-Error')
axes[1].legend()
# axes[0].set_xlim([0, 50])
# axes[0].set_ylim([0, 0.4])
# axes[1].set_xlim([-10, 50])
References
Martin Sandve Alnæs, Anders Logg, and Kent-Andre Mardal. UFC: a finite element code generation interface, pages 283–302. Springer Berlin Heidelberg, 2012. doi:10.1007/978-3-642-23099-8_16.
M. Lenoir. Optimal isoparametric finite elements and error estimates for domains involving curved boundaries. SIAM Journal on Numerical Analysis, 23(3):562–580, jun 1986. doi:10.1137/0723036.