1. Poisson 方程 I#
这里以 Poisson 方程为例, 介绍 Firedrake 的使用, 包括定义有限元空间和变分形式, 施加边界条件, 以及选择不同的数值方法求解线性方程组.
考虑 Poisson 方程
(1.1)#\[\begin{equation}
\begin{aligned}
- \Delta u &= f && x \in \Omega,\\
u &= g_D && x \in \partial\Omega_D, \\
\frac{\partial u}{\partial n} &= g_N && x \in \partial\Omega_N,
\end{aligned}
\end{equation}\]
其中 \(\partial\Omega_D\cap\partial\Omega_N = \partial\Omega\), \(\int_{\partial\Omega_D} {\rm d}s \ne 0\).
定义 试验 和 测试 函数空间
(1.2)#\[\begin{equation}
\begin{aligned}
H_E^1 &:= \{u \in H^1 \,|\, u = g_D \ \ \text{on}\ \ \partial\Omega_D\},\\
H^1_{E_0} &:= \{u \in H^1 \,|\, u = 0 \ \ \text{on}\ \ \partial\Omega_D\}\\
\end{aligned}
\end{equation}\]
Poisson 方程的 变分形式 为
求解 \(u \in H_E^1\), 使得
(1.3)#\[\begin{equation}
\int_\Omega \nabla u\cdot\nabla v = \int_\Omega f v + \int_{\partial\Omega_N} g_N v \qquad \forall v \in H^1_{E_0}.
\end{equation}\]
成立.
1.1. 简单完整示例#
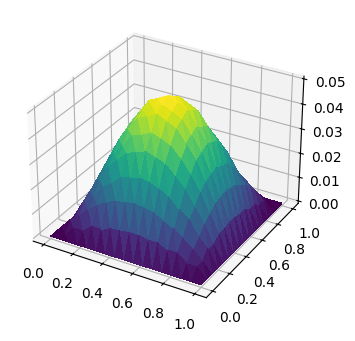
这里我们求解在区域 \(\Omega = (0, 1)\times(0, 1)\) 上的 poisson 问题, 边界条件为齐次迪利克雷边界条件, 即 \(\partial\Omega_N = \emptyset, \partial\Omega_D = \partial\Omega\) 且 \(g_D = 0\).
另外, 我们假设右端源项 \(f = \sin(\pi x)\sin(\pi y)\).
from firedrake import * # Import firedrake
import matplotlib.pyplot as plt
N = 8
test_mesh = RectangleMesh(nx=N, ny=N, Lx=1, Ly=1) # Build mesh on the domain
x, y = SpatialCoordinate(test_mesh)
f = sin(pi*x)*sin(pi*y)
g = Constant(0)
V = FunctionSpace(test_mesh, 'CG', degree=1) # define FE space
u, v = TrialFunction(V), TestFunction(V) # define trial and test function
a = inner(grad(u), grad(v))*dx
L = inner(f, v)*dx # or f*v*dx
bc = DirichletBC(V, g=g, sub_domain='on_boundary')
u_h = Function(V, name='u_h')
solve(a == L, u_h, bcs=bc) # We will introduce other ways to code in the following.
# Plot the result
fig, ax = plt.subplots(figsize=[4, 4], subplot_kw=dict(projection='3d'))
ts = trisurf(u_h, axes=ax)
# You may want to save the figure
# fig.savefig('figures/example.pdf', bbox_inches='tight')
Show code cell output
1.2. Firedrake 中的内置网格#
Firedrake 提供了许多常见几何区域的网格构造函数, 包括矩形, 圆形, 长方体, 球形等.
from firedrake import utility_meshes
print('List of builtin meshes:')
for i, name in enumerate(utility_meshes.__all__):
print(f' {name:<25s}', end='')
if (i+1)%3 == 0:
print('')
List of builtin meshes:
IntervalMesh UnitIntervalMesh PeriodicIntervalMesh
PeriodicUnitIntervalMesh UnitTriangleMesh RectangleMesh
TensorRectangleMesh SquareMesh UnitSquareMesh
PeriodicRectangleMesh PeriodicSquareMesh PeriodicUnitSquareMesh
CircleManifoldMesh UnitDiskMesh UnitBallMesh
UnitTetrahedronMesh BoxMesh CubeMesh
UnitCubeMesh PeriodicBoxMesh PeriodicUnitCubeMesh
IcosahedralSphereMesh UnitIcosahedralSphereMesh OctahedralSphereMesh
UnitOctahedralSphereMesh CubedSphereMesh UnitCubedSphereMesh
TorusMesh CylinderMesh
Tip
How to find the doc or help for functions/classes
?<fun-name>help(<fun-name>)
from firedrake import CubeMesh
help(CubeMesh)
Note
对于复杂的几何区域, 我们可以使用 Gmsh 构造并保存网格, 然后使用函数 Mesh 加载网格.
1.3. Unified Form Language (UFL)#
UFL 是用于表示变分形式的离散化的一门领域特定语言. 它是 FEniCS 项目的一部分.
以下内容摘自 UFL 的文档.
1.3.1. UFL 算子#
下面我们列出常用的 UFL 算子, 更多细节请参考 UFL 的文档 [1].
dot张量缩并,
dot(u, v)对u的最后一个维度和v的第一个维度做缩并.inner张量内积(分量对应乘积之和). 对第二个张量取复共轭.
gradandnabla_gradgrad对张量求导, 新加维度为最后一个维度.
scalar
\[ {\rm grad}(u) = \nabla u = \frac{\partial u}{\partial x_i}{\bf e}_i \]vector
\[ {\rm grad}({\bf v}) = \nabla {\bf v} = \frac{\partial v_i}{\partial x_j}{\bf e}_i \otimes {\bf e}_j \]tensor
设 \(\bf T\) 为秩为 \(r\) 的张量, 那么
\[ {\rm grad}({\bf T}) = \nabla {\bf T} = \frac{\partial {\bf T}_\ell}{\partial x_i}{\bf e}_{\ell_1} \otimes\cdots\otimes {\bf e}_{\ell_r}\otimes {\bf e}_{i} \]其中 \(\ell\) 是长度为 \(r\) 的多指标 (multi-index).
nabla_grad类似
grad, 不过新加维度为第一个维度scalar (same with
grad)\[ {\rm nabla\_grad}(u) = \nabla u = \frac{\partial u}{\partial x_i}{\bf e}_i \]vector
\[ {\rm nabla\_grad}({\bf v}) = (\nabla {\bf v})^T = \frac{\partial v_j}{\partial x_i}{\bf e}_i \otimes {\bf e}_j \]tensor
设 \(\bf T\) 为秩为 \(r\) 的张量, 那么
\[ {\rm nabla\_grad}({\bf T}) = \frac{\partial {\bf T}_\ell}{\partial x_i}{\bf e}_{i}\otimes {\bf e}_{\ell_1} \otimes\cdots\otimes {\bf e}_{\ell_r} \]
divandnabla_divdiv对最后一个维度的偏导数进行缩并.
设 \(\bf T\) 为秩为 \(r\) 的张量, 那么 $\( {\rm div}({\bf T}) = \sum_i\frac{\partial {\bf T}_{\ell_1\ell_2\cdots\ell_{r-1} i}}{\partial x_i}{\bf e}_{\ell_1} \otimes\cdots\otimes {\bf e}_{\ell_{r-1}} \)$
nabla_div类似
div, 不过对第一个维度的偏导数进行缩并.
Note
两个关于梯度的表达式:
\((u\cdot\nabla) v\) →
dot(u, nabla_grad(v))ordot(grad(v), u)\(\Delta u\) →
div(grad(u))
1.3.2. 非线性函数[2]#
abs,signpow,sqrtexp,lncos,sin, ……
1.3.3. Measures#
dx: the interior of the domain \(\Omega\) (dx, cell integral);ds: the boundary \(\partial\Omega\) of \(\Omega\) (ds, exterior facet integral);dS: the set of interior facets \(\Gamma\) (dS, interior facet integral).
在区域内部的边界上积分时, 需要使用 dS 并使用限制算子 + 或 -, 如:
a = u('+')*v('+')*dS
1.3.4. Check UFL form#
from firedrake import *
import ufl
N = 8
test_mesh = RectangleMesh(nx=N, ny=N, Lx=1, Ly=1)
V = FunctionSpace(test_mesh, 'CG', degree=1)
u, v = TrialFunction(V), TestFunction(V)
a = inner(grad(u), grad(v))*dx + inner(Constant(0), v)*dx
print(ufl.formatting.printing.tree_format(a))
Form:
Integral:
integral type: cell
subdomain id: everywhere
integrand:
Conj
Inner
(
Grad
Argument(WithGeometry(FunctionSpace(<firedrake.mesh.MeshTopology object at 0x7f15e03bba00>, FiniteElement('Lagrange', triangle, 1), name=None), Mesh(VectorElement(FiniteElement('Lagrange', triangle, 1), dim=2), 7)), 0, None)
Grad
Argument(WithGeometry(FunctionSpace(<firedrake.mesh.MeshTopology object at 0x7f15e03bba00>, FiniteElement('Lagrange', triangle, 1), name=None), Mesh(VectorElement(FiniteElement('Lagrange', triangle, 1), dim=2), 7)), 1, None)
)
Integral:
integral type: cell
subdomain id: everywhere
integrand:
Product
(
Constant(FiniteElement('Real', None, 0), 12)
Conj
Argument(WithGeometry(FunctionSpace(<firedrake.mesh.MeshTopology object at 0x7f15e03bba00>, FiniteElement('Lagrange', triangle, 1), name=None), Mesh(VectorElement(FiniteElement('Lagrange', triangle, 1), dim=2), 7)), 0, None)
)
1.4. 函数空间创建#
FunctionSpace 标量函数空间
VectorFunctionSpace 向量函数空间
MixedFunctionSpace 混合空间
支持的单元类型: CG, DG, RT, BDM, …
Reference: https://firedrakeproject.org/variational-problems.html#supported-finite-elements
1.5. 线性方程组参数设置#
1.5.1. 添加默认求解参数#
在定义变分形式后, 有三种不同方式进行编码求解
直接使用 solve
先对变分形式进行组装, 然后使用 solve
定义变分问题和变分求解器, 然后求解
下面仍以 Poisson 方程为例进行说明. 相应源文件为 py/possion_example1.py
Tip
可以使用 %load 加载文件内容到 notebook 中
%load py/possion_example1.py
# %load py/possion_example1.py
from firedrake import *
from firedrake.petsc import PETSc
methods = ['solve',
'assemble',
'LinearVariationalSolver']
# Get commandline args
opts = PETSc.Options()
case_index = opts.getInt('case_index', default=0)
if case_index < 0 or case_index > 2:
raise Exception('Case index must be in [0, 2]')
case = methods[case_index]
N = 8
test_mesh = RectangleMesh(nx=N, ny=N, Lx=1, Ly=1)
x, y = SpatialCoordinate(test_mesh)
f = sin(pi*x)*sin(pi*y)
g = Constant(0)
V = FunctionSpace(test_mesh, 'CG', degree=1)
u, v = TrialFunction(V), TestFunction(V)
a = inner(grad(u), grad(v))*dx
L = inner(f, v)*dx # or f*v*dx
bc = DirichletBC(V, g=g, sub_domain='on_boundary')
u_h = Function(V, name='u_h')
if case == 'solve':
PETSc.Sys.Print('Case: solve')
# solve(a == L, u_h, bcs=bc)
solve(a == L, u_h, bcs=bc,
solver_parameters={ # 设置方程组求解算法
# 'ksp_view': None,
'ksp_type': 'preonly',
'pc_type': 'lu',
'pc_factor_mat_solver_type': 'mumps'
},
options_prefix='' # 命令行参数前缀, 这里设为空
)
elif case == 'assemble':
PETSc.Sys.Print('Case: assemble')
A = assemble(a, bcs=bc)
b = assemble(L, bcs=bc)
solve(A, u_h, b,
options_prefix='case2'
)
elif case == 'LinearVariationalSolver':
PETSc.Sys.Print('Case: LinearVariationalSolver')
problem = LinearVariationalProblem(a, L, u_h, bcs=bc)
solver = LinearVariationalSolver(problem,
solver_parameters={
# 'ksp_view': None,
'ksp_monitor': None,
'ksp_converged_reason': None,
'ksp_type': 'cg',
'pc_type': 'none'
},
options_prefix='case3')
solver.solve()
else:
raise Exception(f'Unknow case: {case}')
File('pvd/poisson_example.pvd').write(u_h)
Case: solve
KSP (Krylov subspace solver with preconditioner)
参数: https://petsc.org/main/manual/ksp/#tab-kspdefaults
关于 检查 KSP 的收敛结果请参考下面 4.2 节 KSP.
PC
1.5.2. 命令行参数#
线性方程组的求解还可以通过在命令行添加参数进行控制, 命令行参数将覆盖默认参数. 注意到前面代码中的 options_prefix 参数, 它定义了命令行参数的前缀, 我们将在下面进行解释.
Reference:
参数说明
mat_type:aij或matfreeksp_type: 设置迭代法pc_type: 设置预处理方式pc_factor_mat_solver_type: 设置使用做矩阵分解的包ksp_monitor: 输出每步迭代的残差ksp_view: 迭代完成后输出 ksp 的设置等内容ksp_converged_reason: 输出收敛或不收敛的原因ksp_error_if_not_converged: 不收敛时, 输出错误信息, 并停止.
LU 分解参数设置
Ref:
-ksp_type preonly -pc_type lu -pc_factor_mat_solver_type mumps
选项 pc_factor_mat_solver_type 用于设置 LU 分解使用的 package, 如 petsc, umfpack, superlu, mkl_pardiso, mumps, superlu_dist, mkl_cpardiso 等.
多重网格
终端演示: 设置命令行参数控制线性方程组的求解
下面的三个命令行中, 使用了不同的前缀, 空前缀, case2, 以及 case3
python py/possion_example1.py -case solve \
-ksp_monitor -ksp_converged_reason \
-ksp_type cg -pc_type jacobi
python py/possion_example1.py -case assemble \
-case2_ksp_monitor -case2_ksp_converged_reason \
-case2_ksp_type gmres -case2_pc_type none
python py/possion_example1.py -case LinearVariationalSolver \
-case3_ksp_monitor -case3_ksp_converged_reason \
-case3_ksp_type minres -case3_pc_type none
1.6. 数值积分公式#
1.6.1. 查看数值积分公式#
import FIAT
import finat
from pprint import pprint
ref_cell = FIAT.reference_element.UFCTriangle()
ret = {}
for i in range(0, 4):
qrule = finat.quadrature.make_quadrature(ref_cell, i)
ret[i] = {'points': qrule.point_set.points, 'weights': qrule.weights}
pprint(ret)
{0: {'points': array([[0.33333333, 0.33333333]]), 'weights': array([0.5])},
1: {'points': array([[0.33333333, 0.33333333]]), 'weights': array([0.5])},
2: {'points': array([[0.16666667, 0.16666667],
[0.16666667, 0.66666667],
[0.66666667, 0.16666667]]),
'weights': array([0.16666667, 0.16666667, 0.16666667])},
3: {'points': array([[0.65902762, 0.23193337],
[0.65902762, 0.10903901],
[0.23193337, 0.65902762],
[0.23193337, 0.10903901],
[0.10903901, 0.65902762],
[0.10903901, 0.23193337]]),
'weights': array([0.08333333, 0.08333333, 0.08333333, 0.08333333, 0.08333333,
0.08333333])}}
1.6.2. 显示选择积分公式#
from firedrake import *
import finat
import warnings
# Disable warnings. If we do not do this, there will be warnings:
# UserWarning: Applying str() to a metadata value of type QuadratureRule, don't know if this is safe.
warnings.filterwarnings("ignore", category=UserWarning)
mesh = RectangleMesh(nx=8, ny=8, Lx=1, Ly=1)
V = FunctionSpace(mesh, 'CG', 1)
cell = V.finat_element.cell
x, y = SpatialCoordinate(mesh)
f = x**3 + y**4 + x**2*y**2
ret = {}
for i in range(0, 5):
qrule = finat.quadrature.make_quadrature(cell, i)
ret[i] = {'points': qrule.point_set.points, 'weights': qrule.weights}
v = assemble(f*dx(scheme=qrule))
print(f'degree={i}, v = {v}', )
print('Default: v =', assemble(f*dx(scheme=None)))
warnings.filterwarnings("default", category=UserWarning)
degree=0, v = 0.5579329125675148
degree=1, v = 0.5579329125675148
degree=2, v = 0.5611099431544168
degree=3, v = 0.5611100938585061
degree=4, v = 0.5611111111111102
Default: v = 0.5611111111111102
1.6.3. 自定义数值积分#
from firedrake import *
import FIAT
import finat
import warnings
warnings.filterwarnings("ignore", category=UserWarning)
ref_cell = FIAT.reference_element.UFCTriangle()
print('vertices:', ref_cell.vertices)
point_set = finat.quadrature.PointSet(ref_cell.vertices)
weights = [1/6, 1/6, 1/6]
qrule = finat.quadrature.QuadratureRule(point_set, weights)
print("points: ", qrule.point_set.points)
print("weights: ", qrule.weights)
mesh = RectangleMesh(nx=8, ny=8, Lx=1, Ly=1)
x = SpatialCoordinate(mesh)
print("integral of x[0] on domain by default scheme: ", assemble(x[0]*dx))
print("integral of x[0] on domain by new defined-scheme: ", assemble(x[0]*dx(scheme=qrule)))
vertices: ((0.0, 0.0), (1.0, 0.0), (0.0, 1.0))
points: [[0. 0.]
[1. 0.]
[0. 1.]]
weights: [0.16666667 0.16666667 0.16666667]
integral of x[0] on domain by default scheme: 0.4999999999999994
integral of x[0] on domain by new defined-scheme: 0.4999999999999957
1.7. Dirichlet bounary conditions#
1.7.1. Tags of the boundaries of builtin meshes#
RectangleMesh:
1: plane x == 0
2: plane x == Lx
3: plane y == 0
4: plane y == Ly
from firedrake import *
import matplotlib.pyplot as plt
from py.intro_utils import plot_mesh_with_label
N = 8
rect_mesh = RectangleMesh(nx=N, ny=N, Lx=1, Ly=1)
circ_mesh = UnitDiskMesh(2)
fig, ax = plt.subplots(1, 2, figsize=[8, 4])
plot_mesh_with_label(rect_mesh, axes=ax[0])
plot_mesh_with_label(circ_mesh, axes=ax[1])
fig.tight_layout()
1.7.2. Set Dirichlet boundary conditions#
N = 8
test_mesh = RectangleMesh(nx=N, ny=N, Lx=1, Ly=1)
x, y = SpatialCoordinate(test_mesh)
g = x*2 + y*2
V = FunctionSpace(test_mesh, 'CG', degree=1)
def trisurf_bdy_condition(V, g, sub_domain, axes=None):
bc = DirichletBC(V, g=g, sub_domain=sub_domain)
g = Function(V)
bc.apply(g)
trisurf(g, axes=axes)
if axes:
axes.set_xlabel('x')
axes.set_ylabel('y')
axes.set_title(sub_domain)
# plot the mesh and boundry conditons
fig, ax = plt.subplots(1, 4, figsize=[16, 4], subplot_kw=dict(projection='3d'))
ax = ax.flat
ax[0].remove()
ax[0] = fig.add_subplot(1, 4, 1)
plot_mesh_with_label(test_mesh, ax[0])
ax[0].set_title('mesh')
ax[0].axis('off')
sub_domains = [(1, 2), (3, 4), 'on_boundary']
for i in range(3):
trisurf_bdy_condition(V, g=g, sub_domain=sub_domains[i], axes=ax[i+1])
fig.tight_layout()
1.7.3. sub_domain of DirichletBC#
The following comments are copy from firedrake/bcs.py
# Define facet, edge, vertex using tuples:
# Ex in 3D:
# user input returned keys
# facet = ((1, ), ) -> ((2, ((1, ), )), (1, ()), (0, ()))
# edge = ((1, 2), ) -> ((2, ()), (1, ((1, 2), )), (0, ()))
# vertex = ((1, 2, 4), ) -> ((2, ()), (1, ()), (0, ((1, 2, 4), ))
#
# Multiple facets:
# (1, 2, 4) := ((1, ), (2, ), (4,)) -> ((2, ((1, ), (2, ), (4, ))), (1, ()), (0, ()))
#
# One facet and two edges:
# ((1,), (1, 3), (1, 4)) -> ((2, ((1,),)), (1, ((1,3), (1, 4))), (0, ()))
1.8. Gmsh 网格边界设置#
需要在 gmsh 中给相应的边界加上标签 (Physical Tag)
gmsh gui 演示: 生成如下 geo 文件和 msh 文件
File: gmsh/rectangle.geo
// Gmsh project created on Tue Sep 30 15:09:53 2022
SetFactory("OpenCASCADE");
//+
Rectangle(1) = {0, 0, 0, 1, 1, 0};
//+
Physical Curve("lower", 1) = {1};
//+
Physical Curve("upper", 2) = {3};
//+
Physical Curve("left", 3) = {4};
//+
Physical Curve("right", 4) = {2};
//+
Physical Surface("domain", 1) = {1};
Gmsh file: gmsh/rectangle.msh
from firedrake import *
from firedrake.petsc import PETSc
from py.intro_utils import plot_mesh_with_label
# opts = PETSc.Options()
# opts.insertString('-dm_plex_gmsh_mark_vertices True')
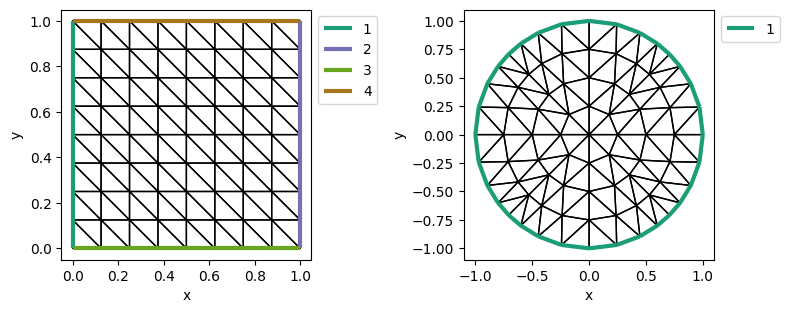
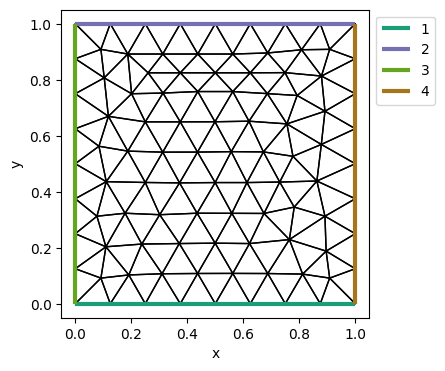
gmsh_mesh = Mesh('gmsh/rectangle.msh')
plot_mesh_with_label(gmsh_mesh)
使用 gmsh 的 python SDK: gmsh 或者 pygmsh
example: py/make_mesh_circle_in_rect.py with gmsh/circle_in_rect.msh
from firedrake import *
from py.intro_utils import plot_mesh_with_label
from py.make_mesh_circle_in_rect import make_circle_in_rect
h = 1/16
filename = 'gmsh/circle_in_rect.msh'
make_circle_in_rect(h, filename, p=3, gui=False)
cr_mesh = Mesh(filename)
plot_mesh_with_label(cr_mesh)
Info : Writing 'gmsh/circle_in_rect.msh'...
Info : Done writing 'gmsh/circle_in_rect.msh'
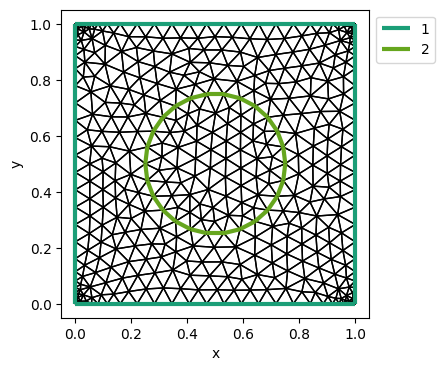
1.9. Neumann boundary condition#
求解如下 Poisson 方程
(1.4)#\[\begin{equation}
\begin{aligned}
- \Delta u &= f &&\quad{\rm in}\quad \Omega,\\
\frac{\partial u}{\partial n} &= g_N &&\quad{\rm on} \quad \partial\Omega,
\end{aligned}
\end{equation}\]
变分问题
求 \(u \in H^1\), 且 \(\int_\Omega u = 0\) 使得
(1.5)#\[\begin{equation}
\int_\Omega \nabla u\cdot\nabla v = \int_\Omega f v + \int_{\partial\Omega} g_N v \qquad \forall v \in H^1.
\end{equation}\]
兼容性条件
\[
\int_\Omega f v + \int_{\partial\Omega} g_N v = 0
\]
1.9.1. Use nullspace of solve#
通过 nullspace 求出的解 u_h 并不满足积分为 0, 而是其对应的解向量的范数最小, 所以我们需要做后处理得到积分为 0 的解:
s = assemble(u_h*dx)/assemble(Constant(1)*dx(domain=mesh)
u_h.assign(u_h - s)
Reference:
from firedrake import *
import matplotlib.pyplot as plt
N = 8
test_mesh = RectangleMesh(nx=N, ny=N, Lx=1, Ly=1)
x, y = SpatialCoordinate(test_mesh)
f = sin(pi*x)*sin(pi*y)
subdomain_id = None # None for all boundray, 或者单个编号 如 1, 或者使用 list 或 tuple 如: (1, 2)
if False:
# 不满足兼容性条件
g = Constant(1)
else:
# 满足兼容性条件
length = assemble(1*ds(domain=test_mesh, subdomain_id=subdomain_id))
g = Constant(-assemble(f*dx)/length)
# g = Constant(-1/pi**2)
V = FunctionSpace(test_mesh, 'CG', degree=1)
u, v = TrialFunction(V), TestFunction(V)
a = inner(grad(u), grad(v))*dx
L = inner(f, v)*dx + inner(g, v)*ds(subdomain_id=subdomain_id)
u1_h = Function(V, name='u1_h')
nullspace = VectorSpaceBasis(constant=True, comm=test_mesh.comm)
solve(a == L, u1_h,
solver_parameters={
# 'ksp_view': None,
'ksp_monitor': None,
},
options_prefix='test1',
nullspace=nullspace,
transpose_nullspace=None)
u2_h = Function(V, name='u2_h')
solve(a == L, u2_h,
solver_parameters={
# 'ksp_view': None,
'ksp_monitor': None,
},
options_prefix='test2',
nullspace=nullspace,
transpose_nullspace=nullspace)
# 通过 nullspace 求出的解并不满足积分为 0, 需要做后处理
omega = assemble(Constant(1)*dx(domain=test_mesh))
s1 = assemble(u1_h*dx)/omega
u1_h.dat.data_with_halos[:] = u1_h.dat.data_ro_with_halos[:] - s1
s2 = assemble(u2_h*dx)/omega
u2_h.dat.data_with_halos[:] = u2_h.dat.data_ro_with_halos[:] - s2
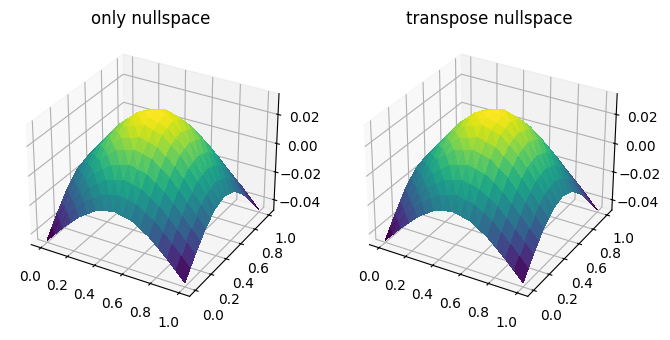
fig, ax = plt.subplots(1, 2, figsize=[8, 4], subplot_kw=dict(projection='3d'))
ts1 = trisurf(u1_h, axes=ax[0])
title1 = ax[0].set_title('only nullspace')
ts2 = trisurf(u2_h, axes=ax[1])
title2 = ax[1].set_title('transpose nullspace')
# plot the error
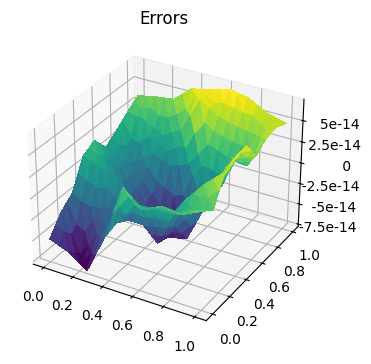
fig, ax = plt.subplots(figsize=[4, 4], subplot_kw=dict(projection='3d'))
err = Function(u1_h).assign(u1_h - u2_h)
trisurf(err, axes=ax)
ax.set_title('Errors')
# The z ticklabel do not show properly, when the values are small.
# we set the major formatter to make it show correctly
fmt = lambda x, pos: f'{x:10g}'
ax.zaxis.set_major_formatter(fmt)
# ax.ticklabel_format(axis='z', style='plain') # may work for not too small values
Residual norms for test1_ solve.
0 KSP Residual norm 9.134205437239e-02
1 KSP Residual norm 2.635631193496e-13
Residual norms for test2_ solve.
0 KSP Residual norm 9.134205437239e-02
1 KSP Residual norm 1.416258567001e-16
1.9.2. Using Lagrange multiplier#
变分问题
求 \(u\in H^1, \mu \in R\) 使得
(1.6)#\[\begin{equation}
\begin{aligned}
& \int_\Omega \nabla u \cdot \nabla v + \mu \int_\Omega v - \int_\Omega f v - \int_{\partial\Omega} g_N v = 0, \quad\forall \in H^1 \\
& \eta \int_\Omega u = 0,\quad \forall \eta \in \mathbb{R}\\
\end{aligned}
\end{equation}\]
File: py/possion_neumann_lagrange.py
# %load possion_neumann_lagrange.py
from firedrake import *
from firedrake.petsc import PETSc
import matplotlib.pyplot as plt
opts = PETSc.Options()
N = opts.getInt('N', default=8)
test_mesh = RectangleMesh(nx=N, ny=N, Lx=1, Ly=1)
x, y = SpatialCoordinate(test_mesh)
f = sin(pi*x)*sin(pi*y)
subdomain_id = None
length = assemble(1*ds(domain=test_mesh, subdomain_id=subdomain_id))
g = Constant(-assemble(f*dx)/length)
# g = Constant(-1/pi**2)
V = FunctionSpace(test_mesh, 'CG', degree=1)
R = FunctionSpace(test_mesh, 'R', 0)
W = MixedFunctionSpace([V, R]) # or W = V*R
u, mu = TrialFunction(W)
v, eta = TestFunction(W)
a = inner(grad(u), grad(v))*dx + inner(mu, v)*dx + inner(u, eta)*dx
L = inner(f, v)*dx + inner(g, v)*ds(subdomain_id=subdomain_id)
w_h = Function(W)
solve(a == L, w_h,
solver_parameters={
# 'mat_type': 'nest',
# 'ksp_view': None,
# 'pc_type': 'fieldsplit',
# 'ksp_monitor': None,
},
options_prefix='test')
u_h, mu_h = w_h.subfunctions
filename = 'pvd/u_h_neumann.pvd'
PETSc.Sys.Print(f'Write pvd file: {filename}')
File(filename).write(u_h)
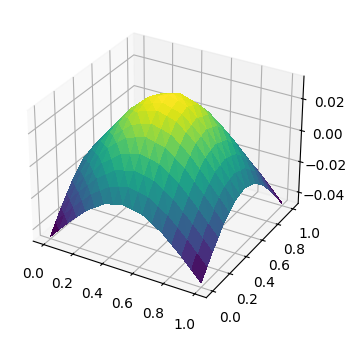
fig, ax = plt.subplots(figsize=[4, 4], subplot_kw=dict(projection='3d'))
ts = trisurf(u_h, axes=ax)
firedrake:WARNING Real block detected, generating Schur complement elimination PC
Write pvd file: pvd/u_h_neumann.pvd
终端演示
$ python possion_neumann_lagrange.py -test_ksp_monitor -test_ksp_converged_reason -N 64
Number of Dofs: 4226
firedrake:WARNING Real block detected, generating Schur complement elimination PC
Residual norms for test_ solve.
0 KSP Residual norm 2.501422711621e-01
1 KSP Residual norm 1.747929427611e-01
2 KSP Residual norm 1.071502741145e-14
Linear test_ solve converged due to CONVERGED_RTOL iterations 2
Write pvd file: pvd/u_h_neumann.pvd
$ mpiexec -n 2 python possion_neumann_lagrange.py \
-test_ksp_monitor -test_ksp_converged_reason -N 64
Number of Dofs: 4226
firedrake:WARNING Real block detected, generating Schur complement elimination PC
Residual norms for test_ solve.
0 KSP Residual norm 2.501422711621e-01
1 KSP Residual norm 2.085403806063e-02
2 KSP Residual norm 9.317076546546e-16
Linear test_ solve converged due to CONVERGED_RTOL iterations 2
Write pvd file: pvd/u_h_neumann.pvd
1.10. 计算收敛阶#
和真解对比
和参考解对比
相邻三层之间对比 (Cauchy 序列): py/possion_convergence.py
1.10.1. 生成网格序列#
base = RectangleMesh(N, N, 1, 1)
meshes = MeshHierarchy(test_mesh, refinement_levels=4)
from firedrake import *
import matplotlib.pyplot as plt
N = 8
base = RectangleMesh(N, N, 1, 1)
meshes = MeshHierarchy(base, refinement_levels=3)
n = len(meshes)
m = min(2, n)
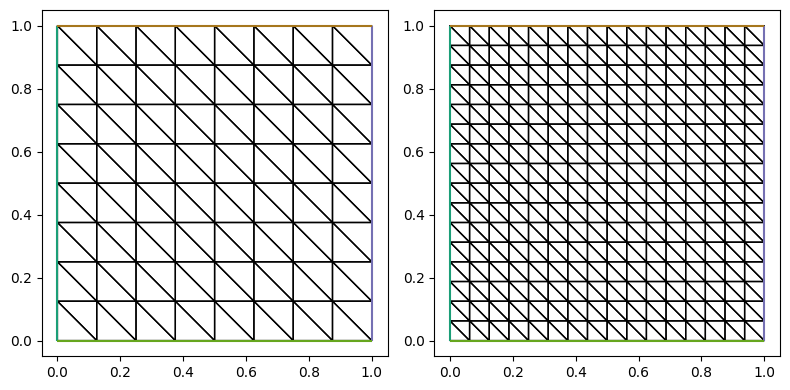
fig, ax = plt.subplots(1, m, figsize=[4*m, 4])
for i in range(m):
triplot(meshes[i], axes=ax[i])
fig.tight_layout()
us = []
for mesh in meshes:
x, y = SpatialCoordinate(mesh)
f = sin(pi*x)*sin(pi*y)
V = FunctionSpace(mesh, 'CG', degree=1)
u = Function(V).interpolate(f)
us.append(u)
m = min(4, n)
fig, ax = plt.subplots(2, 2, figsize=[2*4, 2*4], subplot_kw=dict(projection='3d'))
ax = ax.flat
for i in range(n):
trisurf(us[i], axes=ax[i])
ax[i].set_title(f'$h=1/{N*2**i}$')
1.10.2. 投影到细网格上的空间中#
目前 Firedrake 只能投影函数到相邻层的网格上 (由 MeshHierarchy 生成的网格), 和最密网格比较时可以多次投影, 直至最密网格, 然后比较结果.
下面我们仅比较相邻层的误差
errors = []
hs = []
for i, u in enumerate(us[:-1]):
u_ref = us[i+1]
u_inter = project(u, u_ref.function_space())
error = errornorm(u_ref, u_inter)
errors.append(error)
hs.append(1/(N*2**i))
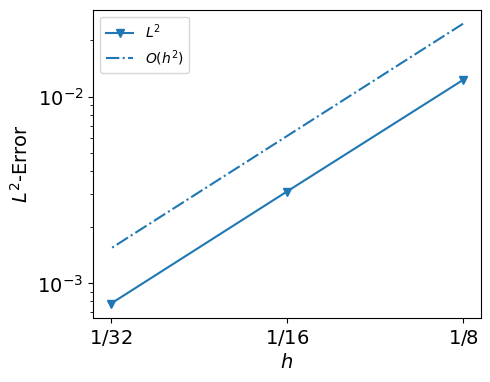
hs, errors
([0.125, 0.0625, 0.03125],
[0.012284003199971312, 0.003100763810085326, 0.00077706141610528])
from py.intro_utils import plot_errors
plot_errors(hs, errors, expect_order=2)
1.10.3. 插值到细网格上的空间中#
VertexOnlyMesh
PointCloud: lrtfm/fdutils
1.10.3.1. Example of PointCloud#
Interpolate function f1 on mesh m1 to function f2 on mesh m2
import firedrake as fd
from fdutils import PointCloud
from fdutils.tools import get_nodes_coords
import matplotlib.pyplot as plt
m1 = fd.RectangleMesh(10, 10, 1, 1)
V1 = fd.FunctionSpace(m1, 'CG', 2)
x, y = fd.SpatialCoordinate(m1)
f1 = fd.Function(V1).interpolate(x**2 + y**2)
m2 = fd.RectangleMesh(20, 20, 1, 1)
V2 = fd.FunctionSpace(m2, 'CG', 3)
f2 = fd.Function(V2)
points = get_nodes_coords(f2)
pc = PointCloud(m1, points, tolerance=1e-12)
f2.dat.data_with_halos[:] = pc.evaluate(f1)
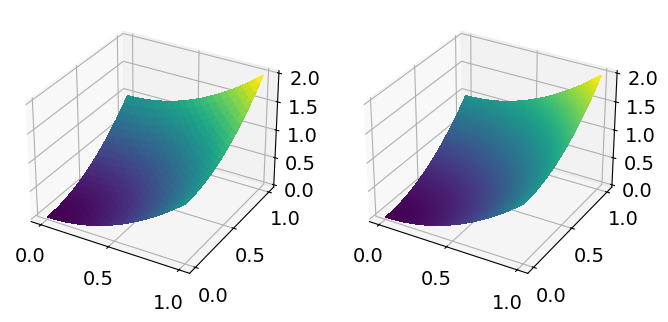
fig, ax = plt.subplots(1, 2, figsize=[8, 4], subplot_kw=dict(projection='3d'))
ts1 = fd.trisurf(f1, axes=ax[0])
ts2 = fd.trisurf(f2, axes=ax[1])
1.10.3.2. 计算误差#
from fdutils.tools import errornorm as my_errornorm
my_errors_0 = []
for i, u in enumerate(us[:-1]):
# 和相邻层结果比较
my_errors_0.append(my_errornorm(u, us[i+1], tolerance=1e-12))
my_errors_0
[0.012284003212205774, 0.003100763847789645, 0.0007770614201378605]
from fdutils.tools import errornorm as my_errornorm
my_errors = []
for i, u in enumerate(us[:-1]):
# 和最密层结果比较
my_errors.append(my_errornorm(u, us[-1], tolerance=1e-12))
my_errors
[0.015349062780286471, 0.003718192030819568, 0.0007770614201378605]
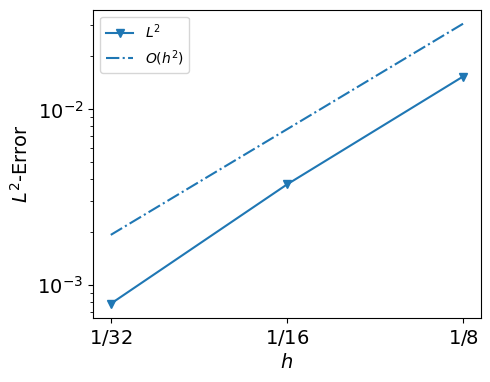
from py.intro_utils import plot_errors
plot_errors(hs, my_errors, expect_order=2)
1.11. 网格尺寸和质量#
1.11.1. 网格尺寸#
网格尺寸 CellDiameter 和 CellSize 一样, 均表示单元的最长边. 函数 MeshGeometry.cell_sizes 是 CellSize 在连续空间 P1 的投影. Circumradius 表示外接圆半径.
Warning
Circumradius 只能用于线性网格
from firedrake import *
mesh = RectangleMesh(1, 1, 1, 1)
V = FunctionSpace(mesh, 'DG', 0)
d = CellDiameter(mesh)
d_int = Function(V).interpolate(d)
r = Circumradius(mesh)
r_int = Function(V).interpolate(r)
size = mesh.cell_sizes
d_int.dat.data, size.dat.data, r_int.dat.data,
(array([1.41421356, 1.41421356]),
array([1.41421356, 1.41421356, 1.41421356, 1.41421356]),
array([0.70710678, 0.70710678]))
1.11.2. 网格质量#
仅作用于线性网格
from firedrake import *
def get_quality_3d(mesh):
kernel = r'''
void get_quality(double coords[4][3], double v[1], double q[1]){
double a, b, c, p;
double ls[6];
double s, r, R, _tmp;
double v1[3], v2[3], v3[3];
int idx[6][2] = {{0, 1}, {2, 3}, {0, 2}, {1, 3}, {0, 3}, {1, 2}};
int idx2[4][3] = {{0, 1, 2}, {0, 2, 3}, {1, 2, 3}, {0, 1, 3}};
for (int i=0; i < 6; i++){
_tmp = 0;
for (int j=0; j < 3; j++){
_tmp += pow(coords[idx[i][0]][j] - coords[idx[i][1]][j], 2.0);
}
ls[i] = sqrt(_tmp);
}
a = ls[0]*ls[1];
b = ls[2]*ls[3];
c = ls[4]*ls[5];
p = (a + b + c)/2;
s = 0;
for (int i=0; i < 4; i++){
for (int j = 0; j < 3; j++){
v1[j] = coords[idx2[i][2]][j] - coords[idx2[i][0]][j];
v2[j] = coords[idx2[i][2]][j] - coords[idx2[i][1]][j];
}
v3[0] = v2[1]*v1[2] - v2[2]*v1[1];
v3[1] = - v2[0]*v1[2] + v2[2]*v1[0];
v3[2] = v2[0]*v1[1] - v2[1]*v1[0];
s += sqrt(pow(v3[0], 2.0) + pow(v3[1], 2.0) + pow(v3[2], 2.0))/2;
}
R = sqrt(p*(p-a)*(p-b)*(p-c))/v[0]/6.0;
r = 3*v[0]/s;
q[0] = r/R;
}
'''
coords = mesh.coordinates
V = FunctionSpace(mesh, 'DG', 0)
volume = Function(V).interpolate(CellVolume(mesh))
quality = Function(V)
cell_node_map = quality.cell_node_map()
op2.par_loop(op2.Kernel(kernel, 'get_quality'), cell_node_map.iterset,
coords.dat(op2.READ, coords.cell_node_map()),
volume.dat(op2.READ, cell_node_map),
quality.dat(op2.WRITE, cell_node_map))
return quality
def get_quality_2d(mesh):
V = FunctionSpace(mesh, 'DG', 0)
quality = Function(V)
kernel = '''
// B[2] - B[0], B[3] - B[1]
// B[4] - B[0], B[5] - B[1]
double S, a, b, c, R, r;
S = fabs((B[5] - B[1])*(B[2] - B[0]) - (B[3] - B[1])*(B[4] - B[0]));
a = sqrt(pow(B[2] - B[0], 2.) + pow(B[3] - B[1], 2.));
b = sqrt(pow(B[4] - B[2], 2.) + pow(B[5] - B[3], 2.));
c = sqrt(pow(B[0] - B[4], 2.) + pow(B[1] - B[5], 2.));
R = a*b*c/(2*S);
r = S/(a+b+c);
A[0] = r/R;
'''
par_loop(kernel, \
dx, \
{'A': (quality, WRITE), 'B' :(mesh.coordinates, READ)})
return quality
def get_quality_2d_surface(mesh):
kernel = r'''
void get_quality(double coords[3][3], double v[1], double q[1]){
double p, _tmp, R, r, ls[3];
double S = v[0];
int idx[3][2] = {{0, 1}, {1, 2}, {0, 2}};
for (int i=0; i < 3; i++){
_tmp = 0;
for (int j=0; j < 3; j++){
_tmp += pow(coords[idx[i][0]][j] - coords[idx[i][1]][j], 2.0);
}
ls[i] = sqrt(_tmp);
}
p = (ls[0] + ls[1] + ls[2])/2;
// S = sqrt(p*(p-ls[0])*(p-ls[1])*(p-ls[2]));
R = ls[0]*ls[1]*ls[2]/(4*S);
r = S/p;
q[0] = r/R;
}
'''
coords = mesh.coordinates
V = FunctionSpace(mesh, 'DG', 0)
volume = Function(V).interpolate(CellVolume(mesh))
quality = Function(V)
cell_node_map = quality.cell_node_map()
op2.par_loop(op2.Kernel(kernel, 'get_quality'), cell_node_map.iterset,
coords.dat(op2.READ, coords.cell_node_map()),
volume.dat(op2.READ, cell_node_map),
quality.dat(op2.WRITE, cell_node_map))
return quality
2d 和 3d
mesh2d = RectangleMesh(1, 1, 1, 1)
mesh3d = UnitCubeMesh(1, 1, 1)
q2 = get_quality_2d(mesh2d)
q3 = get_quality_3d(mesh3d)
q2.dat.data, q3.dat.data
(array([0.41421356, 0.41421356]),
array([0.23914631, 0.23914631, 0.23914631, 0.23914631, 0.23914631,
0.23914631]))
2d 正三角形
from firedrake.petsc import PETSc
from pyop2.datatypes import IntType
import numpy as np
cells = np.array([[0, 1, 2]], dtype=IntType)
coords = np.array([[0.0, 0.0],
[1.0, 0.0],
[1/2, np.sqrt(3)/2]])
plex = PETSc.DMPlex()
plex.createFromCellList(2, cells, coords)
mesh = Mesh(plex)
q_mesh = get_quality_2d(mesh)
q_mesh.dat.data
array([0.5])
曲面网格
mesh_surf = IcosahedralSphereMesh(1)
q_surf = get_quality_2d_surface(mesh_surf)
q_surf.dat.data
array([0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5,
0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5])
from firedrake.petsc import PETSc
from pyop2.datatypes import IntType
cells = np.array([[0, 1, 2]], dtype=IntType)
coords = np.array([[0.0, 0.0, 0.0],
[1.0, 0.0, 0.0],
[1/2, np.sqrt(3)/2, 0.0]])
plex = PETSc.DMPlex()
plex.createFromCellList(2, cells, coords)
mesh = Mesh(plex, dim=3)
q_mesh = get_quality_2d_surface(mesh)
q_mesh.dat.data
array([0.5])